
|
HEALPix conventions
A bandlimited function f on the sphere can
be expanded in spherical harmonics, Ylm,
as
where 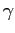 denotes a unit vector pointing at polar angle denotes a unit vector pointing at polar angle
![$\theta\in[0,\pi]$](introimg13.png) and
azimuth and
azimuth
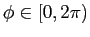 . Here we have assumed that there is insignificant signal power in modes
with l>lmax and introduce the notation that all sums over m run from
-lmax to lmax but all quantities with index lm vanish
for m>l. Our conventions for Ylm are defined in subsection
A.4 below. . Here we have assumed that there is insignificant signal power in modes
with l>lmax and introduce the notation that all sums over m run from
-lmax to lmax but all quantities with index lm vanish
for m>l. Our conventions for Ylm are defined in subsection
A.4 below.
Pixelising 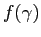 corresponds to sampling it at corresponds to sampling it at 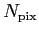 locations
locations 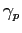 , ,
![$p\in[0,N_{\rm {pix}}-1]$](introimg18.png) . The sample
function values fp can then be used
to estimate alm. A straightforward estimator is . The sample
function values fp can then be used
to estimate alm. A straightforward estimator is
where the superscript star denotes complex conjugation, and an equal weight was assumed for each pixel. This
zeroth order estimator, as well as higher order estimators, are implemented in the
Fortran90 facility anafast, included in the
package. Publications discussing these estimators and the generalised
quadrature problem on the sphere (Hivon et al. ) are in preparation.
Subsections
Eric Hivon
2010-06-18
|

|
