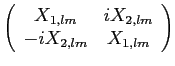|
Relation to previous releases
Even though it was stated otherwise in the documention, HEALPix used a different
convention for the polarization in its previous releases. The tensor harmonics approach
([Kamionkowski et al (1997)], hereafter KKS) was used, instead of
the current spin weighted spherical harmonics. These two approaches differ by
the normalisation and sign of the basis functions used, which in turns change
the normalisation of the power spectra.
Table 1 summarize the relations between the CMB power spectra in the different
releases.
See § A.2 about the interface between HEALPix and CMBFAST.
Table 1: Relation between CMB power spectra conventions used in HEALPix, CMBFAST and
KKS. The power spectra on the same row are equal.
| Component |
HEALPix 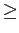 1.21 1.21 |
CMBFAST |
KKS |
HEALPix 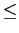 1.12 1.12 |
| Temperature |
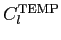 |
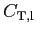 |
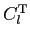 |
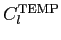 |
| Electric or Gradient |
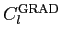 |
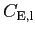 |
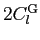 |
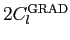 |
| Magnetic or Curl |
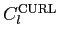 |
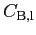 |
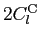 |
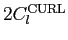 |
| Temp.-Electric cross correlation |
![$C_{l}^{\rm {T-GRAD}}\rule[.3cm]{0cm}{.2cm}$](introimg115.png) |
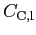 |
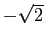
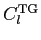 |
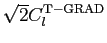 |
|
- 1 Version 1.2 (Feb 2003) or more recent of HEALPix package
- 2 Version 1.1 or older of HEALPix package
|
Introducing the matrices
| Mlm |
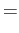 |
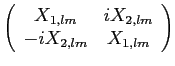 |
(17) |
where the basis functions X1 and X2 have been defined in
Eqs. (10) and above,
the decomposition in spherical harmonics coefficients (9) of a
given map of the Stokes parameter
Q and U can be written in the case of HEALPix 1.2 as
For KKS, with the same definition of M, the decomposition reads
whereas in HEALPix 1.1 it was
The difference between KKS and 1.1 was due to an error of sign on one the basis functions.
Eric Hivon
2010-06-18
|

|