
|
These 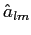 can be used to compute estimates of the angular power spectrum can be used to compute estimates of the angular power spectrum
 as as
The HEALPix package contains the Fortran90 facility synfast
which takes as input a power spectrum Cl and generates a realisation of
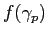 on the HEALPix grid. The convention for power spectrum input into
synfast is straightforward: each Cl is just the expected
variance of the alm at that l.
on the HEALPix grid. The convention for power spectrum input into
synfast is straightforward: each Cl is just the expected
variance of the alm at that l.
Example: The spherical harmonic coefficient a00 is the
integral of the
 over the sphere. To
obtain realisations of functions which have a00 distributed as a Gaussian
with zero mean and variance 1, set C0 to 1. The value of the
synthesised function at each pixel will
be Gaussian distributed with mean zero and variance over the sphere. To
obtain realisations of functions which have a00 distributed as a Gaussian
with zero mean and variance 1, set C0 to 1. The value of the
synthesised function at each pixel will
be Gaussian distributed with mean zero and variance 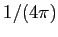 .
As required, the integral of .
As required, the integral of 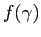 over the full over the full 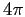 solid angle of the sphere has zero mean and variance
solid angle of the sphere has zero mean and variance 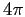 . .
Note that this definition implies the standard result that the total power
at the angular wavenumber l is (2l+1)Cl, because there are
2l+1 modes for each l.
This defines unambiguously how the Cl have to be defined given the
units of the physical quantity f. In cosmic
microwave background research,
popular choices for simulated maps are

 , a dimensionless quantity measuring relative
fluctuations about the average CMB temperature. , a dimensionless quantity measuring relative
fluctuations about the average CMB temperature.
 The absolute quantity
The absolute quantity 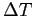 in in 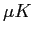 or K. or K.
Eric Hivon
2010-06-18
|

|
