Spherical harmonic conventions

+ View the NASA Portal

Search JPL

Spherical harmonic conventions

The Spherical Harmonics are defined as

$\displaystyle Y_{lm}(\theta,\phi)$

$\textstyle \myequal$

$\displaystyle \lambda_{lm}(\cos\theta) {\rm { e}}^{{i} m\phi}$

(21)

where the

$\displaystyle \lambda_{lm}(x)$	$\textstyle \myequal$	$\displaystyle \sqrt{ \frac{2l+1}{4\pi} \frac{(l-m)!}{(l+m)!} } P_{lm}(x), \quad{\rm for~} m\ge 0$	(22)
$\displaystyle \lambda_{lm}$	$\textstyle \myequal$	$\displaystyle (-1)^m \lambda_{l\vert m\vert}, \quad{\rm for~} m < 0,$
$\displaystyle \lambda_{lm}$	$\textstyle \myequal$	$\displaystyle 0, \quad{\rm for}\, \vert m\vert > l.$

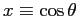Introducing $x\equiv\cos\theta$ , the associated Legendre Polynomials P_lm solve the differential equation

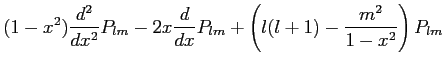$\displaystyle (1-x^2)\frac{d^2}{dx^2}P_{lm} - 2x \frac{d}{dx}P_{lm} + \left(l(l+1) - \frac{m^2}{1-x^2}\right) P_{lm}$

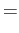$\textstyle \myequal$

(23)

They are related to the ordinary Legendre Polynomials P_l by

P_lm

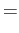$\textstyle \myequal$

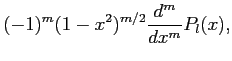$\displaystyle (-1)^m (1-x^2)^{m/2} \frac{d^m}{dx^m} P_{l}(x),$

(24)

which are given by the Rodrigues formula

P_l(x)

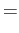$\textstyle \myequal$

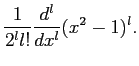$\displaystyle \frac{1}{2^ll!}\frac{d^l}{dx^l} (x^2-1)^l.$

(25)

Note our Y_lm are identical to those of [Edmonds, 1957], even though our definition of the P_lm differ from his by a factor (-1)^m (a.k.a. Condon-Shortley phase).

Eric Hivon 2010-06-18

Contact:

Site Manager:
Webmaster:
CL 03-2650