
|
|
|
|
|

|
|
|
The original motivation for devising HEALPix was one of necessity.
Satellite missions to measure the cosmic microwave background (CMB)
anisotropy - NASA's currently operating
Microwave
Anisotropy Probe (MAP),
and the future ESA mission
Planck
- will produce multi-frequency data
sets sufficient for the construction of full-sky maps of the
microwave sky at an angular resolution of a few arcminutes. The
principal requirements in the development of HEALPix were to
create a mathematical structure which supports a suitable
discretization of functions on a sphere at sufficiently high
resolution, and to facilitate fast and accurate statistical and
astrophysical analysis of massive full-sky data sets.
HEALPix satisfies these requirements because it possesses the
following three essential properties:
-
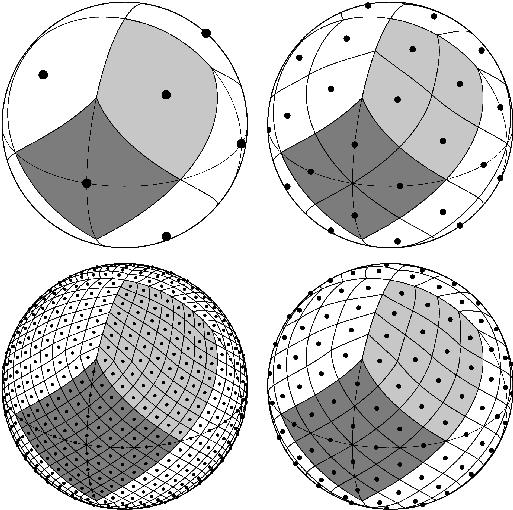
The sphere is hierarchically tessellated into curvilinear
quadrilaterals. The lowest resolution partition is comprised
of 12 base pixels. Resolution of the tessellation increases
by division of each pixel into four new ones. The figure
below illustrates (clockwise from upper-left to bottom-left)
the resolution increase by three steps from the base level
(i.e., the sphere is partitioned, respectively, into 12, 48,
192, and 768 pixels).
-
Areas of all pixels at a given resolution are identical.
-
Pixels are distributed on lines of constant latitude. This
property is essential for all harmonic analysis applications
involving spherical harmonics. Due to the iso-latitude
distribution of sampling points the speed of computation
of integrals over individual spherical harmonics scales as
~N1/2 with the total number of pixels, as opposed to the ~N
scaling for the non-iso-latitude sampling distributions
(examples of which are the
Quadrilateralized Spherical Cube
used for the NASA's
COBE
data, and any distribution based on the symmetries of the icosahedron).
|
|
|
|
|
|
|
|

|
