
|
alm2map_spin*
This routine produces the maps of arbitrary spin s and -s given their alm
coefficients.
A (complex) map S of spin s is a linear combination of the spin weighted harmonics sYlm
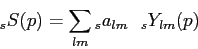 |
(1) |
for
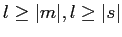 ,
and is such that
sS* = -sS. ,
and is such that
sS* = -sS.
alm2map_spin* expects the alm coefficients to be provided as
| htmlcommentmark>57
|s|a+lm |
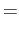 |
- ( |s|alm + (-1)s -|s|alm )/2 |
(2) |
| |s|a-lm |
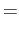 |
- ( |s|alm - (-1)s -|s|alm )/(2i) |
(3) |
for 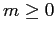 , knowing that, just as for spin 0 maps, the
coefficients for m<0 are given by , knowing that, just as for spin 0 maps, the
coefficients for m<0 are given by
| |s|a+l-m |
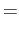 |
(-1)m |s|a+*lm, |
(4) |
| |s|a-l-m |
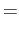 |
(-1)m |s|a-*lm. |
(5) |
The two (real) maps produced by alm2map_spin* are defined respectively as
| |s|S+ |
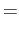 |
(|s|S + -|s|S)/2 |
(6) |
| |s|S- |
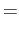 |
(|s|S - -|s|S)/(2i). |
(7) |
With these definitions, 2a+, 2a-, 2S+ and 2S-
match HEALPix polarization aE, aB, Q and U respectively. However, for
s=0,
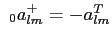 , ,
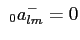 , , 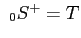 , ,
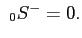
Location in HEALPix directory tree:
src/f90/mod/alm_tools.f90
FORMAT call alm2map_spin*(
nsmax, nlmax, nmmax, spin, alm, map
)
ARGUMENTS
| name & dimensionality |
kind |
in/out |
description |
|---|
| |
|
|
|
|
nsmax |
I4B |
IN |
the Nside value of the map to synthesize. |
| nlmax |
I4B |
IN |
the maximum l value used for the alm. |
| nmmax |
I4B |
IN |
the maximum m value used for the alm. |
| spin |
I4B |
IN |
spin s of the maps to be generated (only its absolute value
is relevant). |
| alm(1:2, 0:nlmax, 0:nmmax) |
SPC/ DPC |
IN |
The
|s|a+lm and
|s|a-lm values to make the map
from. |
| map(0:12*nsmax**2-1, 1:2) |
SP/ DP |
OUT |
|s|S+ and |s|S- output maps |
EXAMPLE:
use healpix_types
use pix_tools, only : nside2npix
use alm_tools, only : alm2map_spin
integer(I4B) :: nside, lmax, mmax, npix, spin
real(SP), dimension(:,:), allocatable :: map
complex(SPC), dimension(:,:,:), allocatable :: alm
...
nside=256 ; lmax=512 ; mmax=lmax ; spin=4
npix=nside2npix(nside)
allocate(alm(1:2,0:lmax,0:mmax))
allocate(map(0:npix-1,1:2))
...
call alm2map_spin(nside, lmax, mmax, spin, alm, map)
Make spin-4 maps from the alm passed in alm. The maps have Nside of 256, and are constructed from alm values up to 512 in l and m.
MODULES & ROUTINESThis section lists the modules and routines used by alm2map_spin*.
-
ring_synthesis
- Performs FFT over m for synthesis of the rings.
-
compute_lam_mm, get_pixel_layout,
-
gen_lamfac_der, gen_mfac, gen_mfac_spin, do_lam_lm_spin,
-
gen_recfac, gen_recfac_spin, init_rescale, l_min_ylm
- Ancillary routines used
for Ylm recursion
-
misc_utils
- module, containing:
-
assert_alloc
- routine to print error message, when an array can not be
allocated properly
RELATED ROUTINESThis section lists the routines related to alm2map_spin*
-
alm2map
- routine generating maps of temperature
and polarisation from their alm
-
alm2map_der
- routine generating maps of temperature
and polarisation, and their spatial derivatives, from their alm
-
map2alm_spin
- routine performing the inverse transform
of alm2map.
-
create_alm
- routine to generate randomly
distributed alm coefficients according to a given power spectrum
Eric Hivon
2010-06-18
|

|
