|
The analysis of functions on domains with spherical topology occupies a
central place in physical science and engineering disciplines.
This is particularly apparent in the fields of astronomy, cosmology,
geophysics, atomic and nuclear physics. In many cases the geometry is either
dictated by the object under study or approximate spherical symmetry can be
exploited to yield powerful perturbation methods. Practical
limits for the purely analytical study of these problems create
an urgent necessity for efficient and accurate numerical tools.
The
simplicity of the spherical form belies the intricacy of global
analysis on the sphere. There is no known
point set which achieves the analogue of uniform sampling in Euclidean space and
allows exact and invertible discrete spherical harmonic decompositions
of arbitrary but band-limited functions. Any existing proposition of practical
schemes for the discrete treatment of such functions
on the sphere introduces some (hopefully tiny)
systematic error dependent on the global properties of
the point set. The goal is to minimise these errors and
faithfully represent deterministic functions as well as realizations of
random variates both
in configuration and Fourier space while maintaining computational efficiency.
We illustrate these points using as an example the field which is particularly
close to the authors' hearts, Cosmic Microwave Background (CMB)
anisotropies. Here we are in the happy situation of expecting an explosion
of available data within the next decade.
The Microwave Anisotropy Probe (MAP) (NASA) and Planck Surveyor (ESA)
missions are aiming
to provide multi-frequency, high resolution, full sky measurements of the anisotropy in
both temperature and polarization of the cosmic microwave
background radiation.
The ultimate data products of these missions --
multiple microwave sky maps, each of which will have to comprise
more than 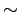 106 pixels in order to render the angular
resolution of the instruments --
will present serious challenges to those involved in the
analysis and scientific exploitation of the results of both surveys. 106 pixels in order to render the angular
resolution of the instruments --
will present serious challenges to those involved in the
analysis and scientific exploitation of the results of both surveys.
As we have learned while working with the COBE mission products,
the digitised
sky map is an essential intermediate
stage in information processing between
the entry point of data acquisition by the
instruments -- very large time ordered data streams,
and the final stage of astrophysical analysis --
typically producing a
'few'
numerical values
of physical parameters of interest.
COBE-DMR sky maps (angular resolution of 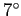 (FWHM) in
three frequency bands, two channels each, 6144 pixels per map)
were considered large at the time of their release. (FWHM) in
three frequency bands, two channels each, 6144 pixels per map)
were considered large at the time of their release.
As for future CMB maps, a whole sky CMB survey
at the angular resolution
of 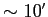 (FWHM), discretised with
a few pixels per resolution element
(so that the discretisation effects on the signal are
sub-dominant with respect to the effects of instrument's angular response),
will require map sizes of at least (FWHM), discretised with
a few pixels per resolution element
(so that the discretisation effects on the signal are
sub-dominant with respect to the effects of instrument's angular response),
will require map sizes of at least
 a few a few
 pixels.
More pixels than that will be needed to represent the Planck-HFI higher
resolution channels.
This estimate, Npix, should be multiplied by the number of frequency bands
(or, indeed, by the number of individual
observing channels -- 74 in the case of Planck -- for the analysis work
to be done before the
final coadded maps are made for each frequency band) to render
an approximate expected
size of the already very compressed form of survey data which would
be the input to the astrophysical analysis pipeline. pixels.
More pixels than that will be needed to represent the Planck-HFI higher
resolution channels.
This estimate, Npix, should be multiplied by the number of frequency bands
(or, indeed, by the number of individual
observing channels -- 74 in the case of Planck -- for the analysis work
to be done before the
final coadded maps are made for each frequency band) to render
an approximate expected
size of the already very compressed form of survey data which would
be the input to the astrophysical analysis pipeline.
It appears to us that very careful
attention ought to be given to devising high resolution CMB map
structures which can maximally facilitate
the forthcoming analyses of large size data sets, for the following
reasons:
 It is clearly very easy to end up with an estimated size of many GBy
for the
data objects which would be directly involved in the science extraction
part of the future CMB missions.
It is clearly very easy to end up with an estimated size of many GBy
for the
data objects which would be directly involved in the science extraction
part of the future CMB missions.
 Many essential scientific questions
can only be answered by global studies of future data sets.
Many essential scientific questions
can only be answered by global studies of future data sets.
This document is an introduction to the
properties of our proposed approach for a high resolution numerical
representation of functions on the sphere
-- the Hierarchical
Equal Area and iso-Latitude Pixelization (HEALPix, see
http://healpix.jpl.nasa.gov),
and the associated multi-purpose computer
software package.
Eric Hivon
2010-06-18
|
